编者按:压缩感知,近几年逐渐从数学和信息科学中独立出来,成为热门的科技新方向,为信号采集技术带来了史无前例的重大突破。究竟何为压缩感知,微软在机器学习计算机领域有哪些研究成果,就让EmmanuelCandes教授为我们一一阐述。
是斯坦福大学的数学、统计学,电子工程荣誉教授,同时也是应用计算数学领域的教授。他的研究领域主要是在这种数学协调分析、数学优化、统计估测,以及在影像科学、信号研究。EmmanuelCandes教授曾获数项国际奖项,包括国家科学基金会最高个人奖项(该奖项主要奖励35岁以下的学者)、2008年信息社会理论论文奖,以及国际行业应用数学学会授予的奖项等等。
点击观看EmmanuelCandes教授的精彩演讲视频:
我想感谢会议主办方,邀请我参加此次会议,我非常高兴能够来到北京,而且我也非常高兴能够见到这么多来自科学计算方面的年轻学子,在这里我主要为大家介绍压缩感知。

目前,我们看到它生成每秒320TB的数据,而它们每秒只能存储1TB的数据,其它的数据怎么办?我们要压缩,把大部分数据扔掉,然后再进行传输。我们要问这样一个问题:我们能否从传感器数据中获得有意义的信号进而直接收集到有用的信息,从而丢弃那些没意义的数据。这就是为什么我要谈压缩感知。现在这种压缩感知是数学理论,我的同事在这个领域有很多贡献。这个压缩感知,主要是利用数据的两个特性:稀疏性以及不连续性,待会我会用一些例子说明。
首先谈到稀疏性,比如说100万象素的图像,怎样才叫做稀疏性的图像呢?比如说我们看到繁星点缀的夜晚,大多数的像素都是黑色的。我们看一下小波变换后的数据,可以看到有些参数的系数非常大,但其中大部份参数的系数都非常小,所以从这个数据我们就能看到这个图像中的稀疏性。这种所谓的稀疏性,让我们能够实现数据压缩。这是原始的图像,我们要扔掉97.5%的子波,让我们来描述一下,然后进行图像重构,然后这就是我们说的数据压缩,百万象素的图像只留下2.5%,也就是最重要的数据,而97.5%的数据都扔掉。(Page8)我们经常谈到不管是音频的,视频的,还是静态的图像都可以这么做。如果我們有一个先验,知道哪里可以收集到大量有用的数据,而哪些是沒有用的。如果我跟他们说我知道信息在哪里,去测量这些数据,而不要测量这些位置,或是他会看到哪些数据是相关的,哪些数据是不相关的。而現在我想问你们的是如果我收集到这些稀疏的数据后,我們要如何去重建原先的東西。如果把这个信息以线性的方式进行测量,然后如何对它进行一个重新的构造呢?
让我们看一下压缩传感知的概念是什么。我们要把未知的信号,也就是我们要获得的信号,由表示为AK。在压缩感知中,AK指的不是一个像素而是一个波型。我们希望它越不连续越好,越扩散越好,而我所要做的是按照一定的顺序获得图像信号的信息。我当时在大学里演讲并展示了我这样的想法后,大家都感到十分奇怪。经由这样的方式收集到的信号是有局部性的,但是整个组合的波型(Waveform)却是具有全局性的,把这些信号联系起来,完全是全局性的信号,每个感测都记录著信号的位置,但是它还是一个比较混乱的现象。我们再来探究一次这个疯狂的提案,我们按照高斯分布来收集数据,而不是线性的,所以我们只会有少量的感测次数,而这些数据的相关性非常低。我有几个来自中国的学生,他们问我像这种的不确定系统的分析,要如何下手?而右手边这些稀疏性的分布曲线代表著什么意义呢?,我要先来找这些系数大,也就是有代表性的系数,但是所有这里边写的这样一种信号,都叫做非零的系数。我们知道解决这个问题的算法,但却需要指数级增长的计算时间,来获得这样一个变化。通过采用一些数据,把其它数据最小化。这些信号是稀疏的,有最小值的,来解决一些在很短时间内出现的问题,这叫做线性编码,在我们这儿进行非常有效的计算。
下面来讲一些压缩传感最基础的东西。压缩的意思,是指比较先前及当前数据的差异,并记录下这些差异而减少需储存的资料量。对于压缩感知的问题比压缩难多了,像是我们要收集怎样分布的数据、如何收集、保留一些什么系数,从而得到最佳的结果。我们会得到一些机变,保留最大的,最有意义的系数在里头。我们可以做一些抽样,把最重要的保留下来。一个信号,我们知道它是非常好的,但这个信号完全是稀疏的,可能并不是我们要损失掉的。让我们看一个图片,这个图片把它的子波设计为零,这个子波有百万象素的,有100万的象素,我们进行9万次不连续的抽样,我们可以看到一个情况,得到一个完全是最初的图片,而且不会失掉任何信息。

![[转载]压缩感知,信号采集的重大突破——记Emmanuel <wbr>Candes教授“21 [转载]压缩感知,信号采集的重大突破——记Emmanuel <wbr>Candes教授“21](http://simg.sinajs.cn/blog7style/images/common/sg_trans.gif) 图2压缩图片的示例
图2压缩图片的示例
我们可以处理更加复杂的对象,比如核磁共振的图像。来看一下这些系数,6000个不连续性系数,我说我们只要看1800不连续的测量,让我们看有什么变化,让我们看看重建后的图片,这些图片是非常接近真实图像的,我们可以用少于三倍或甚至四倍的测量次数而得到一个非常接近的结果。

图3压缩传感在医学影像学中的应用
有什么让我们惊讶的发现呢?它的感应是非常有效的,且为非适应性的。也就是说并不是给你提出20个问题,而且必须看你回答问题的答案之后我们才决定下一题的题目为何,我们不是这样的。我们的测量方式是提前就已经决定好了,我们不用去了解到底这些波型是如何组成的而是以比较被动的方式,我只是把一些信号关联起来,来优化,跟真实比较接近的优化,并不是现实的。第二个令人惊讶的是,可以通过一些可行的方式恢复这个信号。而第三个让我惊讶的则是這個方法非常鲁棒,这也是我今天所想与大家讨论的。把这个信号压缩,再重新解压缩,通过压缩感知来解决这个优化问题。
假设今天你手上有这个稀疏的波型以及经过压缩的信号,你要怎么得到原先的信号呢?答案就是解压缩。我也是一位数学学家,我想你们稍微了解一点我开发的技术,纯数学性的,压缩的感应、机制,抽样的机制,压缩的感应器,连续性,以及稀疏分布如何对应到传感数据的向量。我们要需要传感数据的其中几个特性,像是这个波型的不连续性以及来看一下这些抽样的切入点和顺序。它里面有很多的例子,到底是什么样的一种波形,有可能是非常多噪音的,也可能是随机二元的波型,还有一些选择,像是我选择一个频率,然后給我这个频率的一些相关系数,里面还有很多地方能加以考虑。我们抽样是随机的,而彼此的抽样是沒有相关性的,使用这样最小化一个公式來解这样一个等式,处理这样的一个未定义系统(UndeterminedSystem)。这里边主要的定律,就是如果你的对象是稀疏的,有X度层次的自由度,也就是说大多数的系数为零,但其中有X个系数非零,只要收集次数大于X*LogN的测量就能保证我们可以通过准确的线性编码来恢复,所以你可以看到它的稀疏性是非常关键的,这个信号收集的方法只决定能多靠近真实的数据。这是最近的结果,是基于一般性的,这是我们开发的,如果在你的时间域里边,对有一些稀疏的信号进行抽样,可以这样去做。

图4密集型抽样信号的例子
看一个例子,我们这儿有一个密集型抽样信号,这个信号有这样的一个稀疏的频谱,这个频谱是非常稀疏的。我可以跟你们解释抽样是什么,这样一个数据点,最终我们只要进行很少次数的抽样。这里边不要忘记,也许我涉及到这些稀疏的频谱,要把它尽可能的缩小,然后来恢复重现,可以有这样一个线性的编制,跟最初的信号是完全一样的,这是我们所恢复的波形,得到的结果是我们通过这些抽样,做一些优化,来发挥重要作用,而这些主要跟自由度有关。很多人问我为什么要把它最小化,会不会带来一些灾难性的结果?会不会得到一些根本不存在的信号,这也是为什么我要把能量最小化到零。
下面做什么呢?做一些应用。开始之前我想说,我们压缩感知有很大的工程团队,以及科学的研发工作,然后我们的群体汇集了数学家、统计学家、电路设计学家,还有一些生物医学、影像,包括一些工程,和数学领域结合在一起。
第一个例子,来自于MR,就是核磁共振。我跟你们讲的都是真实的,我想给你们讲一个真实的故事,它是在斯坦福大学的医院里边发生的,有一个男孩,他才两岁,他的健康问题很严重,几个月之前,终于找到捐献的器官来置换这男孩衰竭的肝,但医生对于这男孩的器官是否已经被堵住了这个问题非常关注,非常担心。必须要进行一个高分辨率的扫描,但这个扫描是需要时间的,你得知道这个扫描的过程是非常缓慢的,MRI是非常好的核磁共振获取方式,可以看到其他很多的信息是他种扫描方式所无法得到的,像是CT无法分辨里面的细胞组织是死亡或是活著的。
我们回到这个故事上来,这个两岁的小孩,他来自斯坦福大学医院,MR对这个孩子来说是非常复杂的,他需要做高分辨率的扫描,,如果一边扫描一边呼吸,这个图像就比较模糊了,不能老呼吸,所以这个动作,或任何别的的活动,都会影响到扫描的效果。怎么办呢?必须让他憋着气,不让他喘气,要憋气两分钟,这样才能正确地扫描。两岁的男孩,如果两分钟不呼吸的话,会给他的肝部带来很大问题,所以我们要加速这样一个扫描,从而让MR对小孩身体不造成影响。这些比较复杂数学图形,用这样一个影像,有两个变量,进入到扫描里面,进行计算,会得到一些系数。我们要减少这个扫描时间,怎么抽样这些检验图像,跟那些MRI人讲,他们觉得是不可能的,它是一个规律,但结果是可以做到的,可以看到信息抽象的速度,而不是按照象素抽象。
这是第一个实验,实验开始做压缩传感,这里边有一个恢复原始图像,很多数据是被忽视的,我们需要加速提高6倍,在斯坦福大学医院是可以做到的,在医学的基础上,我们看到这个数据不是稀疏的,我们要最小化,如果要这样做,要完全重建一个图像。在斯坦福大学以及其他的相关机构,需要跟我们结合,ClinicalCoses,他是斯坦福大学一个教授的助理,他用一个系统来加速扫描速度。
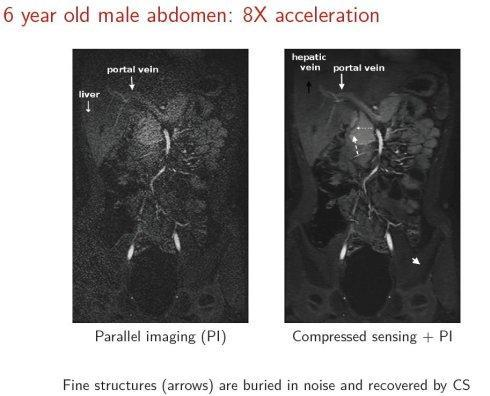
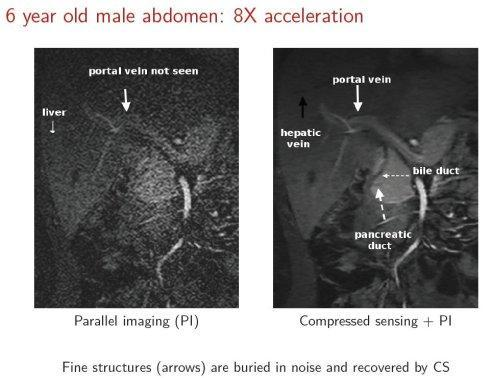
组图 医学影像中的压缩细节
左手边有一些图像,是通过传统扫描技术获得的,右手边可以更加准确,更加细致的看图片,这是8倍的,获得非常可靠的影像,有很多医学影像,图片,这里面有一些压缩细节。有很多箭头,指示一些细节,显示肝损伤的情况。然后会赶上很多工作,我们可以做的就是去减少这种化合物,是8倍的减少,但同时我们可以获得清晰度非常高的图像,从而有助于医生的诊断。这是一个非常严重的肝损害的案例,也就是说我们可以只让病人停止呼吸30秒,而不像以前那样停止呼吸两分钟。主要是因为我们可以加速信号获取的过程,这就是我们谈到的压缩感知,压缩感知可以获得压缩的图形,这样很快的可以获得影像,医生就可以做治疗。这是一个把数学的理论,带到实际临床医疗诊断的应用。
第二个应用,我们开发了一种设备。所有这些都是来自于基金,他们需要开发一个设备,来进行2000兆赫兹频谱里的信号采样,但要收集这些信号的方式就是以频谱两倍的次数进行采样,也就是4000兆赫的采样频率,我们看到信号的频段越来越宽,当信号频段越来越宽的时候,我们就必须相对地提高采样频率,但是要以这种速度来采样是无法达到的。我们知道信号的频谱,我们看到左边更多的信号,以及右边的信号。若是想要得到这种较为尖锐的结果,这个采样的速度和总的带宽是没有关联的。所以这种想法影响了我们实际的模拟转数字的这种数字的转换器的设计,我们看到了很多新的芯片开发出来,他们是想把这种压缩感知做到硬件里,我们所做的一件事情是我们开发了芯片做硬件级的压缩感知,这就是其中的一些芯片。我想传达的信息就是还有很多在这个领域所做的一些工作,这里头是一些比较重要的芯片设计。
再看一下这些芯片,这些芯片可以用于什么领域?可以以一种更快的速度进行高宽带的信号采样。我们来看一下这个架构,其实比较简单。工程师告诉我们,我们无法以原始的方法进行信号采集,但我们可以改变它的波动性,可以通过混合器来做。这个架构我们有输入的高频无线电波,比如说他把信号进行的是一种+1、-1,我们把所有这些系统集成起来采样。我们的芯片就是做这种工作,它所做的就是压缩感知所做的。如果从数学的角度看,当你这样做的时候每一段都是一个随机的序列,我们给这个实验室展示了这样一点,只要我们有一定信号的自由度,我们这样做就不会丢失信息。我们有很多应用像是关于医学方面,有很多电路板的设计采用我们这个理念,这已经成为传感器的应用。这也是一个受到影响的领域,在很多领域都用到了压缩感知,我们知道压缩感知可以带来系统性能的提高。比如说开发了百万象素的照相机,现在有很多摄像头,不光是给你图像,而且给你波长的信息,这样我们就可以降低对整个硬件系统的需求。还有聚焦,加速聚焦速度,我们还可以看到多颜色,甚至还可以有这种压缩银光,有显微镜的效果。
下面我来描述一下一些在机器学习计算机领域对于压缩传感的研究,我的这些同事来自微软研究。这些系数重现用于面部识别,我们看一些人的脸部,如果你看到另一个人,尽管在不同的时间下,我们看到每一段都有相关的象素,它们应该是有关联的。同样一个人的脸在不同的光照下,是一种低秩的结构。我们有这样一个主体,同样的人在不同照明下的图像,我们就可以组成一组数据的矩阵。根据这个理念,我们有新的测试图像,可以应用系数重建来做,它有自己的系数,通过看他的主要的系数我就能知道这个人是怎样的。如果你给我这样一个测试影像,我就把它做一种组合,所有我数据库里这些图像的组合,我要去确定人脸的身份,这张人脸他是白种人。我可以通过系数的取值,看出一个非常干净的画面和比较粗的画面之间的差别,我还可以做一个VIA的等值。我们把它作为一个矢量来看,1是代表错误,如果这样做,他们发现这一个非常让人惊喜的结果,这样的方式能非常准确的预测这个人会是谁,如果把这个图形以这种方式呈现出来,非常好,我们可以看到这样一些向量,然后我们选择同样的图像,就可以获得一系列的向量,这个图像可以进行重新的恢复,以获得一个非常精确的画面。我们看到X的技术,再加上Y的技术,就可以获得很清晰的人脸的图像。
他们将这个概念用于人脸识别,如果他们建一个标准的图像数据库,然后来运行这个算法,来校正这个数据。这一组结果是展示这些简单的算法的性能,他们发现你看到这种校正识别,可以实现60%象素校正。这个时候大家就非常兴奋了,如果有60%的校正系数的话,就可以做很多事情了。
我们谈一些方向问题,我们发展的方向。我再给大家举一个例子,这是美国知名的问题,相信你们之中有人关于机器学习领域的会知道关于这样的问题,我们有这样一个数据库,各种各样的人,各种各样的电影,我们看到对这些电影的评级可以从1到5,1是最差,5是最好,每一个用户都是对很多电影进行打分,所以我们就要来猜一下这个用户,就是说这个用户他还没有看到这个电影,你猜一下这个用户会对这个电影打几分。比如说我们知道这个用户的偏好,这样你就可以建立一个非常高效的预测系统,有一个非常大的数据矩阵,非常稀疏的矩阵,可以从中看到一些已经打出来的分数,我们来进行一个预测,他就是这样一个数据矩阵,我们这个数据矩阵其中有几个是固定的,还有一些是不固定的,有些是缺失的部分,所以看起来这个无法解决,这个问题根本无法回答,但是有一些是已知数,但大部分是未知数,我们怎么来算这个问题。所以我们看一下这和压缩感知要解决的问题是类似的,我们需要什么?需要一个结构。到底我们要做什么结构呢?我们做的这个结构,假设这个数据矩阵它也是一种系数,它不稀疏,我们看到这个结构是录入已知数的,是并不为多的,如果这些未知的矩阵数,也有进行这样一个结构,所以接下来我们看到了一些,已经给出的电影的评级分数,所以未知数比较多,我要去获得一致的样式,我要去找到最低评级。事实上,这个问题比我刚才谈到的影像的问题更加复杂,因为有一个时间的问题,我们要加入一个维数,我们怎么办,我们要去做一个替代算法,我们要把这个L最小化,就像我们在压缩感知上一样,如何用非零进行补充,我们可以恢复一些结构,通过我们在电脑影像方面的方法。下面我放一段视频,这个视频是要做物体跟踪的,通过这样一种建模,这是大堂的监视录像,背景并没有改变,而人在中间持续走动,我们即时地要去分解这些视频,然后恢复一些背景,我们将移动物体和背景分开,我们再放一遍,所以它会自动分辨物体并跟踪移动物体。回到这个幻灯片,确实,我们用了很多工作,使用维数建模。
我来总结一下,我介绍的这种压缩感知,是非常一种有用的协议。如果你们有一些数学方面的点子,来更好的帮助比如说小孩的治疗方案,还有电脑成像学,还有视觉学,确实有很多工作可以做,我欢迎你们和我们研究人员共同开发数学的算法,来改变我们行为的方式。我们一起来开启这场事业吧,谢谢。
相关阅读:
_______________________________________________________________________________
欢迎关注
微软亚洲研究院人人网主页:
微软亚洲研究院微博: